Tam bir zincir ve zincirin bir bölümü için Ohm yasası: formül, açıklama ve açıklama yazma seçenekleri

Profesyonel bir elektrikçinin veya elektronik uzmanının, elektronik ve elektrik devrelerinin kurulumu, ayarlanması ve onarımı ile ilgili sorunları çözerek kendi faaliyetlerinde Ohm yasasını atlamasının hiçbir yolu yoktur.

Aslında herkesin bu yasayı anlaması gerekiyor. Çünkü günlük hayatta herkes elektrikle uğraşmak zorundadır.

Her ne kadar Alman fizikçi Ohm kanunu ortaokul müfredatında yer alsa da, pratikte her zaman zamanında çalışılmıyor. Bu nedenle materyalimizde yaşamla ilgili bu kadar önemli bir konuyu ele alacağız ve formülü yazma seçeneklerini anlayacağız.

Tek bölümlü ve komple elektrik devresi

Ohm yasasını bir devreye uygulama açısından bir elektrik devresi göz önüne alındığında, iki olası hesaplama seçeneğine dikkat edilmelidir: ayrı bir bölüm için ve tam teşekküllü bir devre için.

Bir elektrik devresi bölümünün akımının hesaplanması

Bir elektrik devresinin bir bölümü, kural olarak, ek iç dirence sahip olduğundan, EMF kaynağını hariç tutan devrenin bir parçası olarak kabul edilir.

Bu nedenle, bu durumda hesaplama formülü basit görünüyor:

ben = U/R,

Sırasıyla nerede:

• BEN – mevcut güç;
• sen - uygulanan gerilim;
• R - rezistans.

Formülün yorumlanması basittir - devrenin belirli bir bölümünden akan akım, kendisine uygulanan voltajla orantılıdır ve direnç ters orantılıdır.

Ohm yasasına dayanan tüm formülasyon çeşitlerinin sunulduğu sözde grafik "papatya". Cepte saklama için kullanışlı araç: “P” sektörü - güç formülleri; sektör “U” - voltaj formülleri; sektör “I” - mevcut formüller; sektör “R” - direnç formülleri

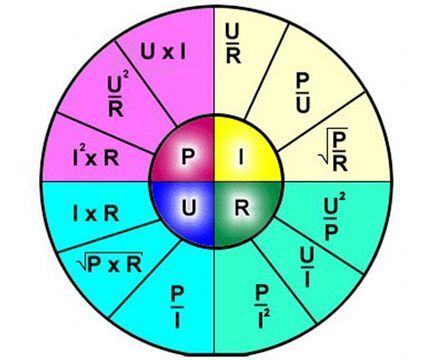
Bu nedenle formül, elektrik devresinin ayrı bir bölümünden geçen akım akışının belirli voltaj ve direnç değerlerine bağımlılığını açıkça açıklar.

Formülün, örneğin voltaj ve akım verildiğinde devreye lehimlenmesi gereken direncin parametrelerini hesaplarken kullanılması uygundur.

Ohm kanunu ve her profesyonel elektromekanik mühendisinin, elektrik mühendisinin, elektronik mühendisinin ve elektrik devrelerinin işleyişiyle ilgilenen herkesin bilmesi gereken iki sonuç. Soldan sağa: 1 - mevcut belirleme; 2 - direncin belirlenmesi; 3 - voltajın tanımı, burada I - akım, U - voltaj, R - direnç

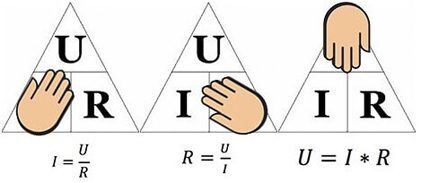
Yukarıdaki şekil, örneğin 12 voltluk bir voltajın uygulandığı 10 ohm'luk bir dirençten akan akımın belirlenmesine yardımcı olacaktır. Değerleri yerine koyarsak – I = 12/10 = 1,2 amper buluruz.

Direnç (akım ve gerilim bilindiğinde) veya gerilim (gerilim ve akım bilindiğinde) bulma problemleri de benzer şekilde çözülür.

Böylece her zaman gerekli çalışma voltajını, gerekli akım gücünü ve optimum direnç elemanını seçebilirsiniz.

Kullanılması önerilen formül, voltaj kaynağının parametrelerinin dikkate alınmasını gerektirmez.Ancak örneğin pil içeren bir devre farklı bir formül kullanılarak hesaplanacaktır. Diyagramda: A – ampermetrenin açılması; V – voltmetreyi açın.

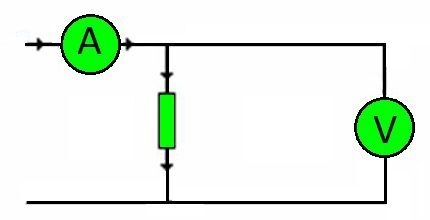
Bu arada, herhangi bir devrenin bağlantı kabloları dirençlerdir. Taşımaları gereken yük miktarı voltaja göre belirlenir.

Buna göre, yine Ohm yasasını kullanarak, çekirdek malzemesine bağlı olarak gerekli iletken kesitini doğru bir şekilde seçmek mümkün hale gelir.

Web sitemizde ayrıntılı talimatlar var kablo kesiti hesaplaması Güç ve akım açısından.

Tam bir zincir için hesaplama seçeneği

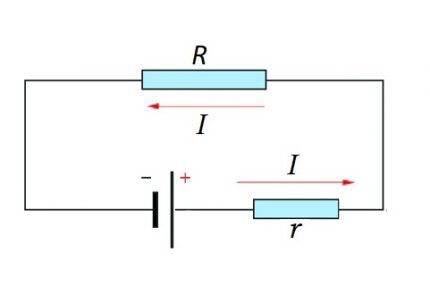
Tam bir devre, bir bölümden (bölümlerden) ve bir EMF kaynağından oluşur. Yani aslında EMF kaynağının iç direnci devre bölümünün mevcut dirençli bileşenine eklenir.

Bu nedenle yukarıdaki formülü biraz değiştirmek mantıklıdır:

ben = U / (R + r)

Tabii ki, Ohm yasasındaki EMF'nin iç direncinin tam bir elektrik devresi için değeri ihmal edilebilir olarak değerlendirilebilir, ancak bu direnç değeri büyük ölçüde EMF kaynağının yapısına bağlıdır.

Ancak karmaşık elektronik devreler, çok iletkenli elektrik devreleri hesaplanırken ek dirençlerin varlığı önemli bir faktördür.

Tam bir elektrik devresi koşulları altında yapılan hesaplamalarda, EMF kaynağının direnç değeri her zaman dikkate alınır. Bu değer, elektrik devresinin kendisinin direnç direnci ile toplanır. Diyagramda: I - akım akışı; R—harici dirençli eleman; r, EMF'nin (enerji kaynağı) direnç faktörüdür

Hem devrenin bir bölümü hem de devrenin tamamı için doğal moment dikkate alınmalıdır - sabit veya değişken akımın kullanılması.

Ohm yasasının karakteristik özelliği olan yukarıda belirtilen noktalar, doğru akımın kullanılması açısından ele alınırsa, alternatif akıma göre her şey biraz farklı görünür.

Kanunun değişken bir miktar üzerindeki etkisinin dikkate alınması

Alternatif akımın geçme koşullarına karşı “direnç” kavramı daha çok “empedans” kavramı gibi düşünülmelidir. Bu, dirençli bir yükün (Ra) ve reaktif direnç yükünün (Rr) kombinasyonunu ifade eder.

Bu tür olaylara, endüktif elemanların parametreleri ve değişken bir voltaj değeri - sinüzoidal bir akım değeri - ile ilgili olarak anahtarlama yasaları neden olur.

Bu, Ohm yasası ilkelerine dayalı formülasyonlar kullanılarak hesaplamaya yönelik alternatif akım elektrik devresinin eşdeğer devresidir: R - dirençli bileşen; C kapasitif bileşendir; L—endüktif bileşen; EMF bir enerji kaynağıdır; ben - akım akışı

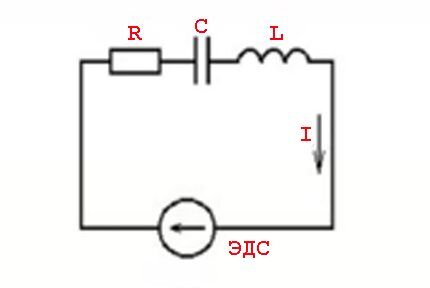
Başka bir deyişle, aktif (dirençli) ve reaktif (endüktif veya kapasitif) güçlerin ortaya çıkmasıyla birlikte, akım değerlerinin gerilim değerlerinden önde (gecikme) etkisi vardır.

Bu tür olaylar aşağıdaki formül kullanılarak hesaplanır:

Z=U/I veya Z = R + J * (X_L -X_C)

Nerede: Z - iç direnç; R – aktif yük; X_L , X_C – endüktif ve kapasitif yük; J - katsayısı.

Elemanların seri ve paralel bağlantısı

Bir elektrik devresinin elemanları (bir devrenin bölümü) için karakteristik nokta, seri veya paralel bağlantıdır.

Buna göre, her bağlantı tipine farklı bir akım akışı ve voltaj besleme modeli eşlik eder.Bu bakımdan Ohm kanunu da elemanların dahil edilme seçeneğine bağlı olarak farklı şekilde uygulanır.

Seri bağlı dirençli elemanların devresi

Seri bağlantıyla (iki bileşenli bir devrenin bölümü) ilgili olarak aşağıdaki formülasyon kullanılır:

• ben = ben₁ = ben₂ ;
• sen = sen₁ +U₂ ;
• R = R₁ + R₂

Bu formülasyon, seri olarak bağlanan dirençli bileşenlerin sayısına bakılmaksızın, devrenin bir bölümünden akan akımın değerinin değişmediğini açıkça göstermektedir.

Devrenin bir bölümündeki dirençli elemanların birbirleriyle seri olarak bağlanması. Bu seçeneğin kendi hesaplama yasası vardır. Diyagramda: I, I1, I2 - akım akışı; R1, R2 - dirençli elemanlar; U, U1, U2 - uygulanan voltaj

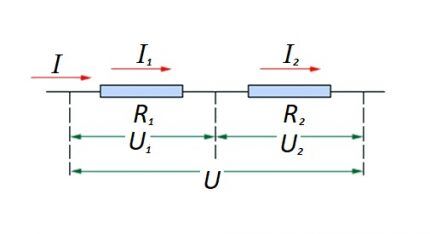
Devrenin etkin dirençli bileşenlerine uygulanan voltajın büyüklüğü, emk kaynağının değerinin toplamıdır ve toplamıdır.

Bu durumda, her bir bileşenin voltajı şuna eşittir: Ux = I * Rx.

Toplam direnç, devredeki tüm dirençli bileşenlerin değerlerinin toplamı olarak düşünülmelidir.

Paralel bağlı dirençli elemanların devresi

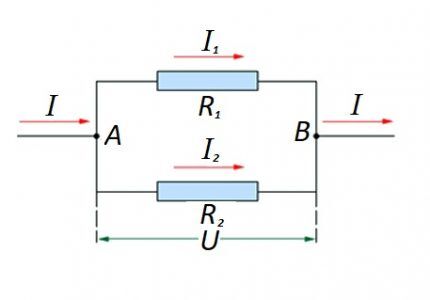
Dirençli bileşenlerin paralel bir bağlantısının olması durumunda, aşağıdaki formülasyon Alman fizikçi Ohm yasasına göre adil kabul edilir:

• ben = ben₁ +ben₂ … ;
• sen = sen₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Paralel ve seri bağlantılar kullanıldığında "karışık" tipte devre bölümleri oluşturma seçenekleri hariç tutulmaz.

Bir devrenin bir bölümündeki dirençli elemanların birbirine paralel bağlanması. Bu seçenek için farklı bir hesaplama kanunu uygulanır. Diyagramda: I, I1, I2 - akım akışı; R1, R2 - dirençli elemanlar; U sağlanan voltajdır; A, B - giriş/çıkış noktaları

Bu tür seçenekler için hesaplama genellikle başlangıçta paralel bağlantının direnç değerinin hesaplanmasıyla gerçekleştirilir. Daha sonra elde edilen sonuca seri bağlanan direncin değeri eklenir.

Hukukun integral ve diferansiyel biçimleri

Hesaplamalarla birlikte yukarıdaki noktaların tümü, elektrik devrelerinde tabiri caizse "homojen" yapıdaki iletkenlerin kullanıldığı koşullar için geçerlidir.

Bu arada, pratikte, iletkenlerin yapısının farklı bölümlerde değiştiği şemaların yapımıyla sık sık uğraşmak gerekir. Örneğin, daha büyük kesitli veya tersine farklı malzemelerden yapılmış daha küçük teller kullanılır.

Bu tür farklılıkları hesaba katmak için "diferansiyel-integral Ohm yasasının" bir çeşidi vardır. Sonsuz küçük bir iletken için akım yoğunluğu seviyesi, gerilim ve iletkenlik değerine bağlı olarak hesaplanır.

Diferansiyel hesaplama için aşağıdaki formül kullanılır: J = ό * E

İntegral hesaplaması için buna göre formülasyon şu şekildedir: ben * R = φ1 – φ2 + έ

Ancak bu örnekler yüksek matematik okuluna oldukça yakındır ve aslında basit bir elektrikçinin gerçek uygulamasında kullanılmaz.

Konuyla ilgili sonuçlar ve faydalı videolar

Aşağıdaki videoda Ohm yasasının ayrıntılı bir analizi, nihayet bilginin bu yönde pekiştirilmesine yardımcı olacaktır.

Benzersiz bir video dersi teorik yazılı sunumu niteliksel olarak güçlendirir:

Bir elektrikçinin işi veya bir elektronik mühendisinin faaliyeti, kişinin Georg Ohm yasasını uygulamalı olarak gerçekten gözlemlemesi gereken anlarla bütünsel olarak bağlantılıdır. Bunlar her profesyonelin bilmesi gereken bazı gerçeklerdir.

Bu konuda kapsamlı bilgi gerekli değildir - pratikte başarılı bir şekilde uygulamak için ifadelerin üç ana varyasyonunu öğrenmek yeterlidir.

Yukarıdaki materyali değerli yorumlarınızla desteklemek veya fikrinizi ifade etmek ister misiniz? Lütfen yorumlarınızı makalenin altındaki bloğa yazınız. Sorularınız varsa uzmanlarımıza sormaktan çekinmeyin.